Axial-length computation using corneal dimensions and A-scan biometry
Rey Matanguihan, MD, James Co Shu Ming, MD, Processo Surrell, MD
THE INTRODUCTION of new technologies such as ultrasound and the keratometer has made it possible to measure the axial length and corneal curvature for estimating intraocular-lens (IOL) power. Subsequent largescale population studies have led to the development of linear regression formulas, the most popular of which is the SRK II formula named after its authors Sanders, Retzlaff, and Kraff. These new technologies are hardly available in many areas in the Philippines. For instance, most of the 700 or so cataract surgeries performed in outreach surgical missions by the Department of Ophthalmology of the East Avenue Medical Center were done without the use of automated biometry machines. Many of these surgeries used IOLs within 20 to 22 D. La Nauze showed in a study of 346 Vietnamese adults that the mean IOL power for emmetropia was 20.72 D for males and 21.94 D for females.1 About 95% of their study population were within 5.5 D of these mean results. No similar study on Filipinos has been published. The need for a system of determining a suitable IOL without relying on biometry machines was addressed by Processo Surrell in a 2002 pilot study where he used a formula for computing IOL power based on measurements of the corneal diameter and height.2 He based his computations on two assumptions: the eyeball is composed of two unequal spheres (corneal and sclera) fused at the limbus; the sclera covers 300 degrees while the cornea covers the rest. He then devised a formula for axial-length computation based on a system of triangles and principles of the Pythagorean system as follows:

In a study of 30 eyes, Surrell found no significant statistical difference between biometry readings and the axial length, keratometry, and IOL power derived from this formula. Determination of axial length is an important step in IOL estimation. As early as 1992, Olsen had already noted in a study of 584 IOL implantations that as much as 54% of the error was attributed to axial-length discrepancies.3 Since then, few studies have explored the relationship of the cornea and axial length. Touzeau compared biometric parameters measured with Orbscan with the subjective spherical equivalent of 190 eyes of 95 patients.4 Corneal biometric parameters did not correlate with refractive error but a strong correlation between corneal radius and axial length was seen. Yebra-Pimentel found a direct relationship between the axial-length-to-corneal-radius (AL/CR) ratio and the refractive error in hyperopes, emmetropes and low myopias.5 This study compared computed axial length using Surrell’s formula with readings retrieved from automated biometry measurements using the A-scan. We hypothesized that the results of the two methods would be the same and may then be used in subsequent studies of IOL determination using clinical measurements.
METHODOLOGY
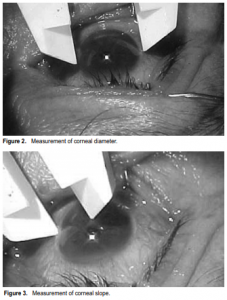
This is a comparative, nonrandomized study of patients from the outpatient department of a tertiary-care academic medical institution who were screened for cataract surgery from April 1, 2004 to September 1, 2004. Patients with a history of eye trauma and ocular surgery and those previously diagnosed with gross abnormalities of size and shape of the cornea and sclera were excluded. Main outcome measures were corneal diameter, corneal slope, and axial length. The corneal diameter and slope were measured at the outpatient department. The patients were made to lie supine on a flat bed. Topical anesthesia was administered and a lid retractor placed. The horizontal and vertical corneal diameters were measured (Figure 2) using the anterior edge of the gray transition zone between the clear cornea and limbus as landmarks at the 3 and 9 o’clock and 6 and 12 o’clock positions under a microscope with a plastic Vernier caliper (Hangzhou Jinnan Tools and Measure Co. Ltd., China). The caliper is accurate up to 0.05 millimeter. The corneal slope is the distance measured from the center of the cornea to the landmarks of the gray transition zone at the 3, 6, 9, and 12 o’clock positions (Figure 3). Corneal measurements were done 3 times by a single examiner and results were encoded in MS Excel (Microsoft Corporation, Redmond, Washington, USA). The axial lengths were computed using Surrell’s formula for eachof the 4 meridians and the average axial length was labeled as the “Computed AXL.” Corresponding axial-length values were measured three consecutive times by another masked observer using Ophthasonic A-Scan III machine (Teknar Ophthasonic A-scan III, Teknar, St. Louis, MO, USA) and the values were recorded as “Measured AXL.” All data were recorded up to one-hundredth of a millimeter. The precision of computed axial length was defined as standard deviation of the difference between computed and measured axial-length values. Student t test compared the average of the “Computed AXL” values versus the average “Measured AXL” at p < 0.05 for statistical significance, using SPSS 10.0 for Windows (SPSS Inc., Chicago, IL, USA).
RESULTS
A total of 105 eyes (96 patients; 47 males, 49 females; ages 20 to 78) were included in the study. Computed axial lengths ranged from 21.10 to 24.41 mm, with a mean of 22.94 mm ± 0.65 mm (Table 1). Measured axial lengths ranged from 20.81 to 26.43 mm, with a mean of 23.06 mm ± 0.99 mm. Figure 4 shows a plot of the computed axial lengths with the corresponding measured axial length in ascending order.
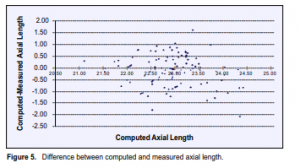
The mean difference between measured and computed axial was +0.12mm ±0.66 mm (range of -1.62 to +2.08 mm). Figure 5 shows a scatter graph plotting the difference between measured and computed axial length values. A positive or negative value means that the computed axial length was either overestimated or underestimated compared with the corresponding A-scan measurement. The difference between computed and measured axial lengths for the whole study population was not statistically significant (p = 0.08, 95% CI). Neither was the difference statistically significant for axial lengths less than 22.00 mm (p = 0.64), 22.00 to 22.99 mm (p = 0.11), 23.00 to 23.99 mm (p = 0.81). However, the difference was significant for axial length of 24.00 mm or greater (p = 0.03) (Table 1).

DISCUSSION
The results indicate that the axial length obtained from measurements of the corneal diameter and slope approximates that obtained by A-scan biometry. The results are important in relation to the determination of IOL power. When applying the SRK II formula to compute for the difference in IOL power using the mean computed and measured axial lengths for the whole subject population, the 0.12 mm difference translates to a 0.30 diopter IOL discrepancy. The diopter IOL discrepancy was 0.175 (from mean difference of 0.07 mm) in the group with computed axial length of < 22.00 mm, 0.325 (from mean difference of 0.14 mm) in the group with computed axial length of 22.00 to 22.99 mm, 0.075 (from mean difference of 0.03 mm) in the group with computed axial length of 23.00 to 23.99 mm, and 1.875 (from mean difference of 0.75 mm) in eyes with computed axial length of 24.00 mm and greater. Although the methodology is simple, interobserver
variability may exist and alter the computed axial length due to differences in identifying corneal/limbal landmarks, the positioning of the caliper, and reading the measurements on the scale. Surell’s formula assumes that the cornea and the globe are two unequal perfect spheres. In reality, imperfections in the actual shape of the eyeball become sources of error when calculating for the axial length this way. This is obviated with direct ultrasound measurements in the A-scan method. In summary, this study showed that axial-length computation using the Surell formula can reliably approximate the actual axial length measured by A-scan and, in cases where an ultrasound machine is not available, may be used to determine the correct IOL power for
patients about to undergo cataract surgery.
References
1. La Nauze J, Kim Thanh T, et al. Intraocular-lens-power prediction in a Vietnamese population: a study to establish a limited set of intraocular-lens powers that could be used in a Vietnamese population. Ophthalmic Epidemiology 1999; 6:147-158.
2. Surrell P, Co Shu Ming J, Del Mundo J. Formulas based on geometric properties of the eye in intraocular-lens-power calculation. Phillippine Academy of Ophthalmology. http://www.pao.org.ph/main.php?fid=annual/abs2002bt7.
3. Olsen T. Sources of error in intraocular-lens-power calculation. J Cataract Refract Surg 1992; 18: 125-129.
4. Touzeau O, Allouch C, Borderie V, et al. Correltion entre la refraction et la biometrie oculaire. J Fr Ophthalmol 2003; 26:355-363.
5. Yebra-Pimentel E, Giraldez MJ, Glez-Meijome JM, et al. Variacion de la ratio longitud axial/radio corneal (LA/CR) con el estado refractivo ocular. Relacion con los
componentes oculares. Arch Soc Esp Oftalmol 2004; 79: 317-324.
6. Bron AJ, et al. Wolff’s Anatomy of the Eye and Orbit, 8th ed. Arnold Publishing, 1997; 211-214.
7. Sayegh FN. The correlation of corneal refractive power, axial length, and the refractive power of the emmetropizing intraocular lens in cataractous eyes. Ger J Ophthalmol 1996; 5: 328-331.
8. Raj PS, Ilango B, Watson A. Measurement of axial length in the calculation of intraocular-lens power. Eye 1998; 12: 227-229.

